- Intro
1.1 Source Code - Boards / Cells
- Row/Column/House Traversal
- Candidate Analysis
4.1 Update Candidates / Single Candidate Elimination
4.2 Hidden Single Candidate Elimination - Backtracking
- Conclusion
This article discusses Pseudokude (pseudocode + sudoku), an algorithm made in Rust for solving sudoku boards of any size up to a u16. Pseudokude makes use of backtracking as well as candidate analysis.
1.1 Source Code
Pseudokude makes use of two different objects, the Board object, and the Cell object.
The Board object represents an entire sudoku board, including its size, the size of its houses, what the last modified Cell was, and most importantly, it contains a 2D vector of Cell objects.
The Cell object represents individual cells, containing its digit, the coordinates of all other cells in its row/column/house, as well as all of its candidates and banned candidates.
To allow for backtracking and candidate analysis, a cell must be able to compile a list of all its surrounding cells to determine what possible digits it could be. These lists are the vectors row, col, and house. There is an additional list titled aoe for "area of effect", which is defined as the union of row, col, and house, $ \text{row}\cup \text{col}\cup \text{house} $.
Special care is taken to ensure that the cell's own coordinates are not included in any of these lists. See Board.init() below, which initializes all cells. Note that color functionality have been removed from this codeblock and all other codeblocks in this article. See also the visualization of each cell's area-of-effect.
//Initialize values of board from given input, where init is the sudoku board. fn init(&mut self, init: &Vec<Vec<u16>>) { let mut hx: usize; let mut hy: usize; //Iterate through row for i in 0..self.bsize { //Initialize row self.cell.push(Vec::new()); //Iterate through column for j in 0.. self.bsize { //Initialize cell self.cell[i].push(Cell::new()); //Assign digit to cell self.cell[i][j].digit = init[i][j]; //Initialize row and column coordinates for k in 0..self.bsize { if k != j { self.cell[i][j].row.push([i,k]); } if k != i { self.cell[i][j].col.push([k,j]); } } //The top-left coordinate for the cell's house hy = (((i/self.hsize) as f64).floor() as usize)*(self.hsize); hx = (((j/self.hsize) as f64).floor() as usize)*(self.hsize); //Iterate from top-left of house and add to cell's house and aoe coordinates. for k in 0..self.hsize { for l in 0..self.hsize { if i != (k+hy) || j != (l+hx) { self.cell[i][j].house.push([(k+hy),(l+hx)]); self.cell[i][j].aoe.push([(k+hy),(l+hx)]); } } } //Initialize AOE coordinates for k in (self.hsize-(j%self.hsize)+j)..self.bsize { self.cell[i][j].aoe.push([i, k]); //Row after house } for k in 0..(j+(self.hsize-(j%self.hsize))-self.hsize) { self.cell[i][j].aoe.push([i, k]); //Row before house } for k in (self.hsize-(i%self.hsize)+i)..self.bsize { self.cell[i][j].aoe.push([k, j]); //Column after house } for k in 0..(i+(self.hsize-(i%self.hsize))-self.hsize) { self.cell[i][j].aoe.push([k, j]); //Column before house } } } }

Candidate analysis has three steps: updating each cell's individual candidates, searching for cells that contain only one candidate, and determining whether a cell's candidate is unique to at least one of its areas.
4.1 Update Candidates / Single Candidate Elimination
Before a cell can be eliminated, we must first determine its candidates. This is done by iterating through and compiling all digits from the cell's area-of-effect.
Every cell's candidate list is updated all at once when the board is first loaded as well as when popping the Board stack during backtracking. When filling in a cell, only that cells within the area-of-effect are updated. This stand-alone update is where single candidate elimination occurs.
Below is the pseudocode for update_cand(). Note that this function is recursive. If a single candidate elimination is possible, then this function is further called for all cells in that coordinate's area. Another very similar version of this function exists that updates all candidates, update_all_cand(), the code for which is almost exactly the same as the following code.
FUNCTION update_cand(cell)
FOR each empty coordinate in the cell's area of effect
CLEAR coordinate's candidates
APPEND all free digits to the coordinate's candidates
IF coordinate has only 1 candidate THEN
SET coordinate's digit to that candidate
update_cand(coordinate)
END IF
END FOR
END FUNCTION
See the Rust code for update_cand() below. To gather what digits are in a cell's area, the additional function coords_to_digits() is used. coords_to_digits() is multi-purpose, as it is also used for obtaining all candidates within a cell's area, which will be required for 4.2.
//Updates the candidates of all cells, restricted by cand_limit. fn update_cand(&mut self, coord: [usize; 2]) { let mut aoe: Vec<u16>; //Current cell's house let mut cand_len: u16; for each in &self.cell[coord[0]][coord[1]].aoe.clone() { if self.cell[each[0]][each[1]].digit == 0 { cand_len = 0; self.cell[each[0]][each[1]].cand.clear(); //Assign all candidates, restricted by limit and cand_limit. aoe = self.coords_to_digits(&self.cell[each[0]][each[1]].aoe, false); for k in 1..(self.bsize+1) { if !aoe.contains(&(k as u16)) && !self.cell[each[0]][each[1]].cand_limit.contains(&(k as u16)) { self.cell[each[0]][each[1]].cand.push(k as u16); cand_len += 1; } } //If there is only 1 candidate, set it as the digit and update further cells. if cand_len == 1 { self.cell[each[0]][each[1]].digit = self.cell[each[0]][each[1]].cand[0]; self.update_cand([each[0], each[1]]); } } } }
//Returns a vector of digits OR candidates from a vector of coordinates fn coords_to_digits(&self, area: &Vec<[usize; 2]>, return_cand: bool) -> Vec<u16> { let mut output: Vec<u16> = vec![]; //Iterate through area for each in area { //Whether to return area's digits or all of area's candidates if return_cand { if self.cell[each[0]][each[1]].digit == 0 { for each in &self.cell[each[0]][each[1]].cand { output.push(*each); } } } else { if self.cell[each[0]][each[1]].digit != 0 { output.push(self.cell[each[0]][each[1]].digit); } } } return output; }
4.2 Hidden Single Candidate Elimination
Single hidden candidate elimination is the process of determining whether a cell has a candidate that is unique to its row, column, or house. If a candidate only exists within a single cell in an area, then that cell must be that candidate, regardless of whether or not the cell has other candidates and regardless of whether or not that digit exists as a candidate in the other areas.
The following is an example of a cell that can be solved using hidden single candidate elimination.
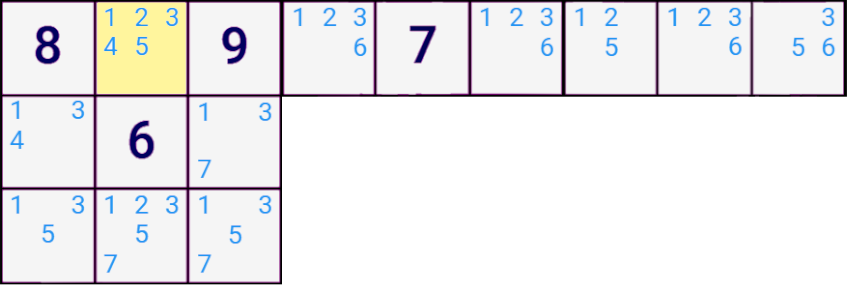
Credit to smartsudoku.com for image.
Note that the highlighted cell has multiple candidates, however it is the only cell in its row that has 4 as a candidate. This means it must be 4, which further decreases the candidates in the house as shown below.
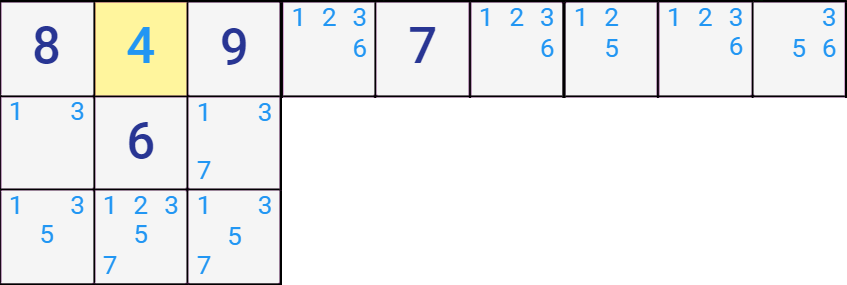
Credit to smartsudoku.com for image.
The function process_of_elimination() is shown below, which is responsible for single hidden candidate analysis. Note that the function makes use of update_cand() from 4.1.
FUNCTION process_of_elimination()
WHILE there are potentially more eliminations DO
FOR each empty cell on the board
FOR each of cell's candidates
FOR each coordinate in cell's areas (row, column, and house)
IF candidate exists in area THEN CONTINUE
SET digit to candidate
update_cand(coordinate)
END FOR
END FOR
END FOR
END WHILE
END FUNCTION
The Rust code for the function process_of_elimination() is also below. Note that the function makes use of update_cand() and coords_to_digits() from 4.1.
//Checks for cells that have candidates that are unique to one of its areas fn process_of_elimination(&mut self) { let mut c: u16; //Current cell's candidate let mut row: Vec<u16>; //Current cell's row let mut col: Vec<u16>; //Current cell's col let mut house: Vec<u16>; //Current cell's house let mut reset: bool = true; //Whether or not to keep searching //Start search while reset { self.solved = true; reset = false; //Iterate through all cells for i in 0..self.bsize { for j in 0..self.bsize { //Ensure cell is a 0 if self.cell[i][j].digit == 0 { self.solved = false; //Establish candidates in each area row = self.coords_to_digits(&self.cell[i][j].row, true); col = self.coords_to_digits(&self.cell[i][j].col, true); house = self.coords_to_digits(&self.cell[i][j].house, true); //If areas do not contain candidate, then set cell to candidate. for k in 0..self.cell[i][j].cand.len() { c = self.cell[i][j].cand[k]; if !row.contains(&c) || !col.contains(&c) || !house.contains(&c) { self.cell[i][j].digit = c; self.update_cand([i, j]); reset = true; } } } } } } }
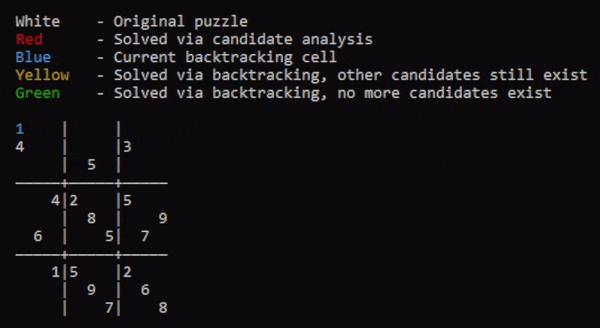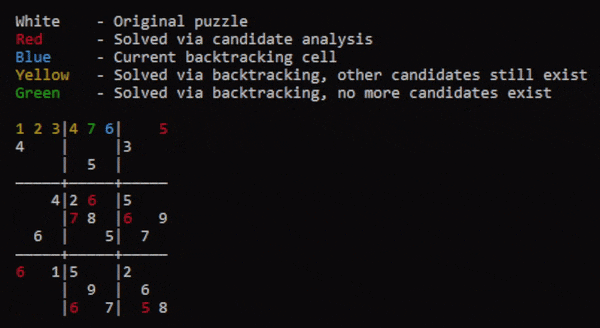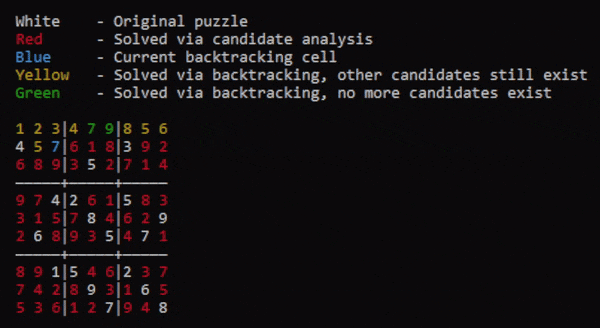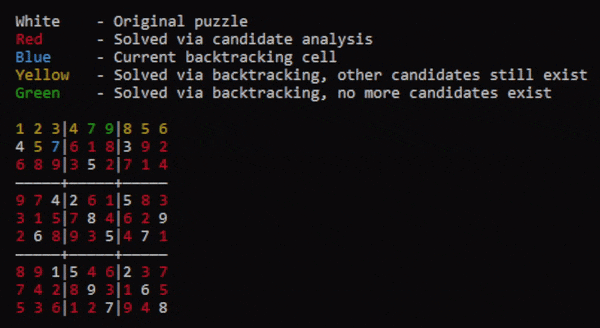
Candidate analysis is extremely effective for most sudoku puzzles, but as the board size increases and the amount of given information decreases, more advanced strategies must be implemented. In the case of Pseudokude, backtracking is used starting from the top-left of the board and working its way to the right.
Pseudokude uses a fairly standard backtracking algorithm. For every board iteration, a new copy of the board is pushed to a stack. If the board is determined to be unsolvable, then the stack is popped and the most recently backtracked cell gets its digit added to its list of banned candidates and resets, ensuring that branch is never traversed again.
Below is the pseudocode for the backtracking algorithm used. This is the main algorithm of Pseudokude, as it makes use of all the previous functions described. Note that the condition for popping is encountering a cell that is empty but that has zero candidates. This only occurs if the board is impossible to solve.
SET board equal to the board to be solved
SET board_stack to a stack of boards
board.init()
board.update_all_cand()
board.process_of_elimination()
PUSH board to board_stack
WHILE the board isn't solved DO
SET board to the top of board_stack
FOR each empty cell in board
IF cell has candidates THEN
SET cell to the first of its candidates
SET board's last_modified to cell's coordinate and digit
board.update_cand(cell)
board.process_of_elimination()
PUSH board to board_stack
ELSE THEN
POP board_stack
PUSH top of stack's last_modified digit to its cell's banned candidate list
SET top of stack's last_modified cell to empty
top of board_stack.update_all_cand()
top of board_stack.process_of_elimination()
CONTINUE outer WHILE loop
END IF
END FOR
END WHILE
Below is the Rust code for backtracking, which is just Pseudokude's main() function. Some functionality has been stripped from this example code, including color functionality and error checking.
//Main code containing backtracking logic. fn main() { //The board to be solved. let init = vec![ vec![1,2,0,3,0,0,0,0,0], vec![4,0,0,0,0,0,3,0,0], vec![0,0,3,0,5,0,0,0,0], vec![0,0,4,2,0,0,5,0,0], vec![0,0,0,0,8,0,0,0,9], vec![0,6,0,0,0,5,0,7,0], vec![0,0,1,5,0,0,2,0,0], vec![0,0,0,0,9,0,0,6,0], vec![0,0,0,0,0,7,0,0,8]]; let mut b = Board::new(init.len()); //The main board let mut b_stack: Vec<Board> = vec![]; //The stack of boards b.init(&init); //Initialize cells and area coordinates b.update_all_cand(); //Update the candidates for all cells b.process_of_elimination(); //candidates initialization b_stack.push(b.clone()); //Push first unsolved board to stack. //Main back-tracking loop while b.solved == false { //Update temporary board b = b_stack.last_mut().unwrap().clone(); //Iterate through cells 'outer: for i in 0..b.bsize { for j in 0..b.bsize { //Ensure cell is a 0 if b.cell[i][j].digit == 0 { //Ensure cell has candidates if b.cell[i][j].cand.len() > 0 { //Set cell to first candidate and update the last-modified cell data. b.cell[i][j].digit = b.cell[i][j].cand[0]; b.last_modified = [i, j, b.cell[i][j].cand[0] as usize]; //Update candidates and check for area candidate eliminations. b.update_cand([i, j]); b.process_of_elimination(); //Push board to stack b_stack.push(b.clone()); //No candidates mean the current board state is impossible to solve. } else { //Pop top of stack. b_stack.pop(); //Revert the last-modified cell to a 0 and update its cand_limit list. b_stack.last_mut().unwrap().cell[b.last_modified[0]][b.last_modified[1]].cand_limit.push(b.last_modified[2] as u16); b_stack.last_mut().unwrap().cell[b.last_modified[0]][b.last_modified[1]].digit = 0; //Update candidates and check for area candidate eliminations. b_stack.last_mut().unwrap().update_all_cand(); b_stack.last_mut().unwrap().process_of_elimination(); //Restart search break 'outer; } } } } } //Show the solved board b_stack.last_mut().unwrap().show(); }
There are some optimizations that could be made to Pseudokude. I could've implemented solving methods such as the X-Wing Strategy, but I felt that it would have been nothing but more of the same in regard to the challenge of implementing it. Alternative optimizations include using a single-coordinate system (versus working with an x and a y) and using bitwise operations for determining candidates (this comes at the cost of not being able to solve boards wider than 64 cells).
Overall I consider Pseudokude a success. It has been a very fun exercise in code optimization and problem solving. Again, be sure to check out the source code over on GitHub.