Fast Random Pathfinder

Jul 30, 2024

Intro
1.1 Source Code
Random Pathfinding Algorithm
2.1 Finding a Random Path
2.2 Filling the Path
2.3 Optimizing the Path
The Disadvantages
3.1 Map Size/Terrain
3.2 Impossible Optimizations
3.3 Worst Case Runtime
Bonus: Maze Generation

1. Intro

This article discusses the development of a "fast" pathfinder that operates via random traversal.

It should be said that there is little use for a pathfinder that relies solely on random chance when traversing. This project exists solely for curiosity's sake, and should not ever be considered for actual use cases when alternatives like A* exist.

1.1 Source Code

Source code on GitHub

2. Random Pathfinding Algorithm

An easy and almost instinctual solution to developing a random pathfinder is to simply move in random directions until reaching the goal. While this is algorithmically simple, it is far too computationally inefficient. In my testing, pathfinding by moving to random immediately adjacent directions often yields paths consisting of millions of steps even for miniscule 20x20 mazes.

That is why an alternative random pathfinding algorithm will be explored, the Fast Random Pathfinder. This algorithm is still truly random in its solution, but it is much faster.

2.1 Finding a Random Path

Fast Random Pathfinder operates by checking whether any two distinct points on the map can see each other without any obstructions between. In this implementation, a simple grid is used alongside DDA raycasting for determining whether any two points have sight-line of each other.

Cells on the map are randomly selected and checked for whether they have sight-line to the last node in the path. If they can see each other, then that random cell gets added to the path as a node and the process continues until the goal is in sight.

This is the key to Fast Random Pathfinder's efficiency compared to randomly moving to open adjacent cells. Although time is lost from checking many cells that wind up intersecting with walls, the nodes that are found are often far away, allowing for faster traversal and an ultimately shorter path.

WHILE the last node in path[] cannot see the goal
    randomNode = a random position on the map
    IF randomNode can see the last node in path[] THEN
        APPEND randomNode to path[]
    END IF
END WHILE
APPEND goal to path[]

View the drop-downs below to see the C++ code for findPath(), which selects random nodes, and canSee(), which determines node visible using DDA raycasting. Some functionality has been stripped from how these normally operate within fast-random-pathfinder.cpp in order to make their use in this specific case more apparent.

findPath() C++ Code

/**
@brief Finds a path using random movement.
This function begins in the top left of the map and finds a random path to the
goal at the bottom right of the map.
*/
void findPath() {
	vector <int> node = {2 + (rand() % (mapH-3)), 2 + (rand() % (mapW-3))}; //The node to be checked
	path.push_back({2,2}); //The starting point
	vector <int> goal={mapH-3, mapW-3}; //The goal
	int orig_state=0; //Holds the original color of cells
	//Loops until the goal is reached
	while(true) {
		node = {2 + (rand() % (mapH-3)), 2 + (rand() % (mapW-3))}; //Sets what node is to be checked
		//Checks that the node isn't a wall or the same as the previous node
		if(map[node[0]][node[1]] != 0 && node != path[path.size()-1]) {
			//If the goal is in sight, then exit search.
			if(canSee(path[path.size()-1], goal, false)) {
				break;
			}
			//If the node is in sight, add it to the path, otherwise revert its color.
			if(canSee(path[path.size()-1], node)) {
				path.push_back(node);
			}
		}
	}
	//Add goal to the very end of path.
	path.push_back(goal);
	
}

canSee() C++ Code

/*
@brief Checks cell visibility and can fill path between cells.
This function determines whether two cells on the grid have sightline of each other using DDA traversal.
@param prev: The first cell to check.
@param next: The second cell to check.
@return boolean of whether the given cells could see each other.
*/
bool canSee(vector <int> prev, vector <int> next) {
	//Current coords
	double x = prev[1];
	double y = prev[0];
	//Previous coords
	double px=x;
	double py=y;
	//The starting coords
	double startx=x;
	double starty=y;
	//Target coords
	double tx = next[1];
	double ty = next[0];
	//The difference between the start and target
	double dx=0;
	double dy=0;
	//Used to hold DDA calculations
	double fracx;
	double fracy;
	double frac;
	//Used for checking corner-skips.
	vector <int> cc_xy = {0, 0};
	//Loop until the x and y encounter a wall.
	while(map[int(y)][int(x)] != 0) {
		//Check whether the target has been reached.
		if(int(x) == int(tx) && int(y) == int(ty)) {
			return true;
		}
		
		//Set the difference between the start and target.
		dx=tx-x;
		dy=ty-y;
		
		//DDA traversal
		if(abs(dx) >= abs(dy)) {
			frac = abs(dx);
		} else {
			frac = abs(dy);
		}
		fracx = dx / frac;
		fracy = dy / frac;
		x += fracx;
		y += fracy;
		//Checks that the DDA didn't squeeze through a corner.
		if(int(px) != int(x) && int(py) != int(y) && addToPath == false) {
			cc_xy[0] = 0, cc_xy[1] = 0;
			if(dy > 0) {
				cc_xy[1] = -1;
			} else {
				cc_xy[1] = 1;
			}
			if(dx > 0) {
				cc_xy[0] = -1;
			} else {
				cc_xy[0] = 1;
			}
			if(map[int(y)+cc_xy[1]][int(x)] == 0 && map[int(y)][int(x)+cc_xy[0]] == 0) {
				break;
			}
		}
		//Set the current x & y to be used later as the previous x & y.
		px=x;
		py=y;
	}
	return false;
	
}

The traversal of a path generated using this algorithm is visualized below. This path had a total of 8969 nodes before reaching the goal, which is exponentially faster than any path that the originally discussed random-direction-based-algorithm would've been able to consistently generate.

2.2 Filling the Path

Now that a path has been found, we fill in the spaces between nodes that are not immediately adjacent to the previous node. This provides more options for optimization later.

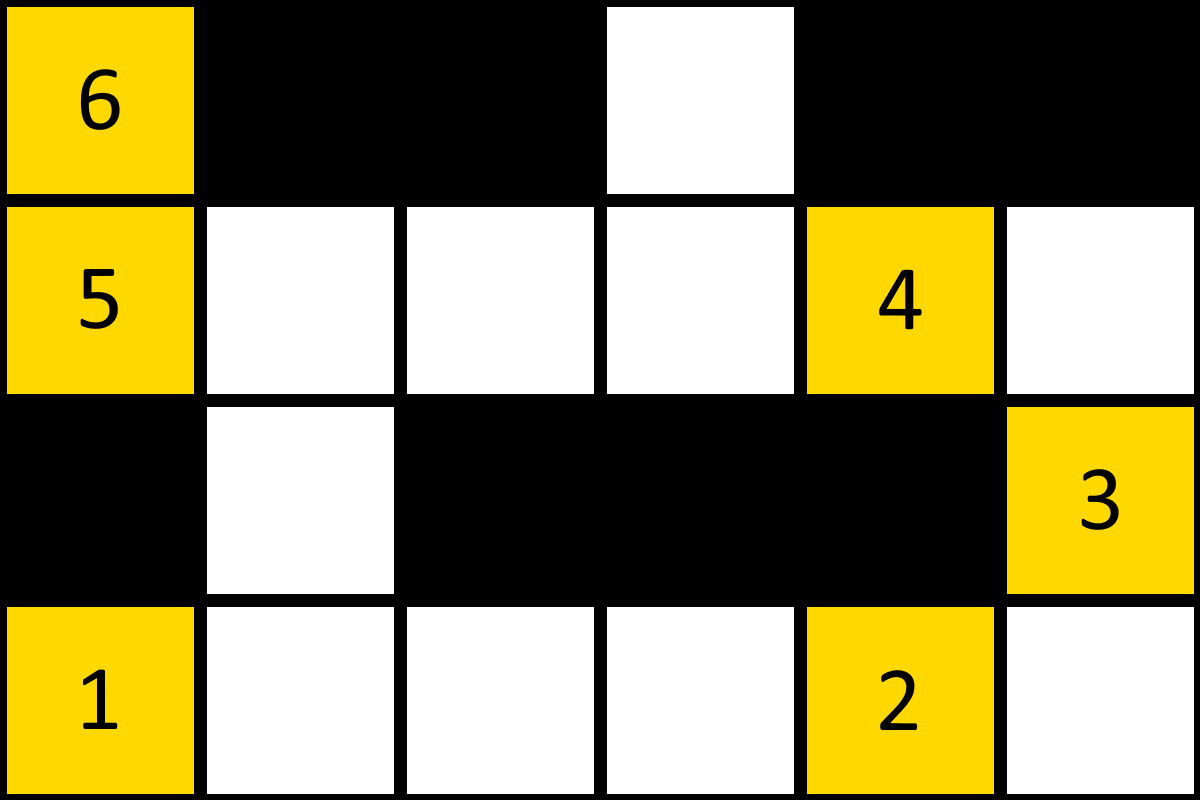
The above image is an example of a random path which has no available optimizations, each node can only see the next node ahead and the previous node behind. We can increase the number of potential optimizations by filling in the spaces between the nodes with new nodes, as shown below.

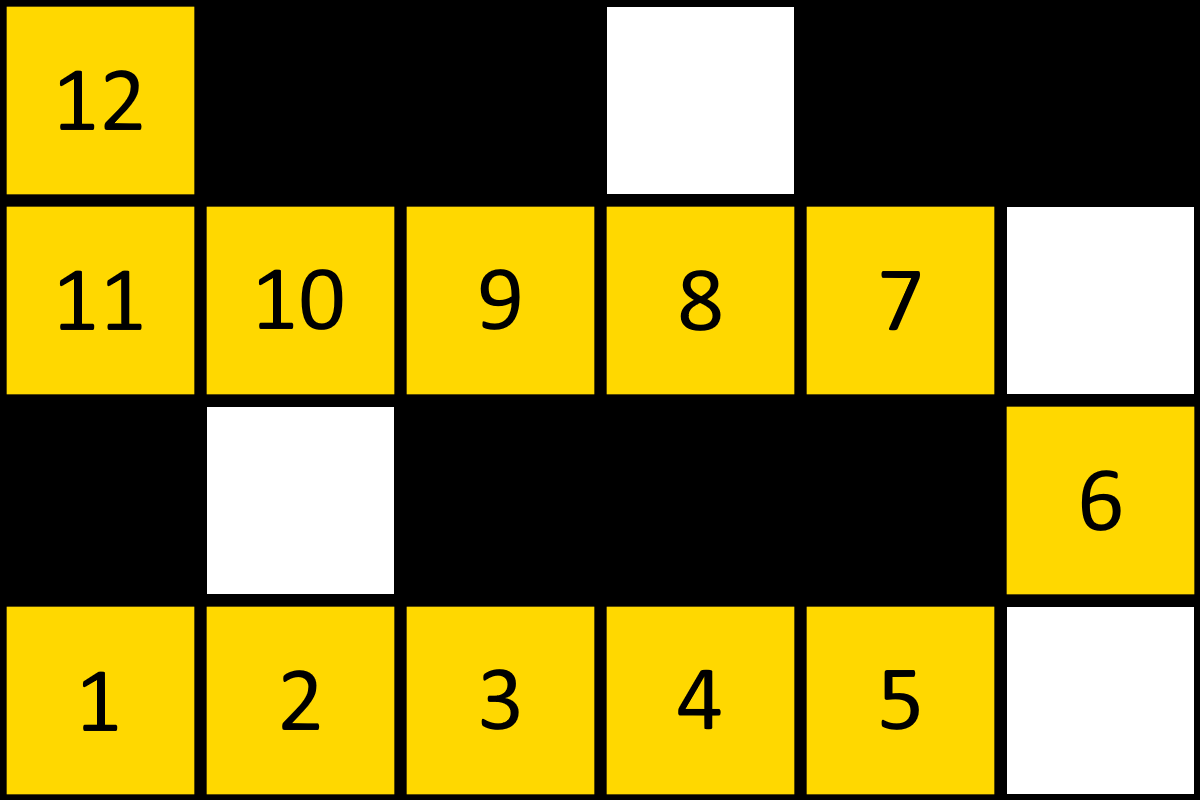
Nodes 1 and 9 now have sight-line of each other. This means that the other nodes can be trimmed from the path, which will be expanded upon in 2.3.

FOR each node in path[], i
    IF path[i] and path[i+1] are not immediately adjacent THEN
        INSERT all the cells between the nodes path[i] and path[i+1]
    END IF
END FOR

2.3 Optimizing the Path

Finally, we iterate forwards and backwards through the path and find nodes that can be skipped entirely. We erase these nodes from the path until no more optimizations can be made. Here is the previous example after being optimized.

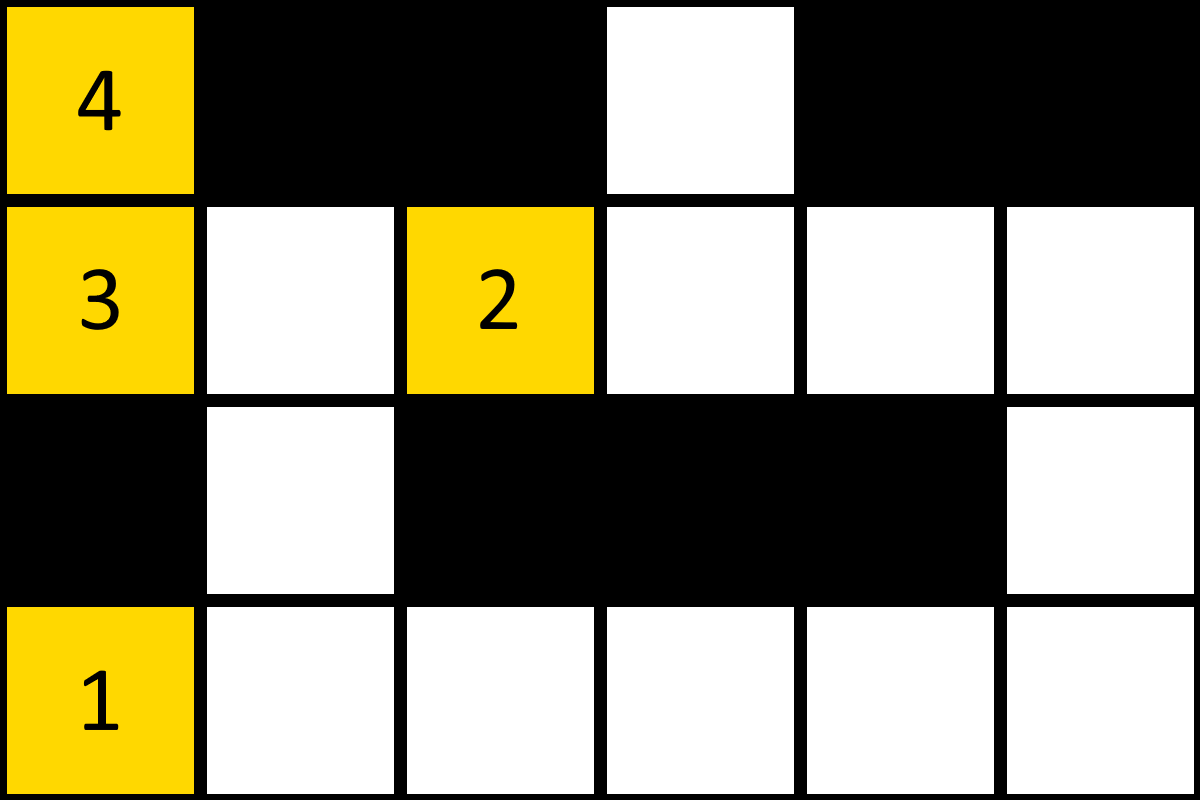
Note that this is not the most optimal path between the first and last nodes, but it is the only one that Fast Random Pathfinder is able to find given its linear nature. This is further discussed in 3.2.

FOR each node at the start of path[] moving forwards, i
    FOR each node at the end of path[] moving backwards, j
        IF i-j=1 THEN
            BREAK
        END IF
        IF path[i] can see path[j] THEN
            ERASE the nodes between i and j in path[]
        END IF
    END FOR
END FOR

View the drop-down below to see the C++ code for optimizePath(). Note the use a goto rather than an outer while-loop. By using goto, the outer for-loop can be broken and restarted from within the inner for-loop without the need of an additional method or variable.

optimizePath() C++ Code

/*
@brief Optimizing the initially found path.
This function iterates through each cell in the path. For each cell, it iterates
backwards from the very end the path and checks whether the initial cell and any
of the cells after can see eachother. If they can, then any cells between them
are erased from the path list and the search restarts until no optimizations can
be made.
*/
void optimizePath() {
	optimizePathRestart: ; //Used if the entire search needs to restart.
	//Iterate forward from the start of the path.
	for(int i = 0; i < path.size(); i++) {
		//Iterate backwards from the end of the path.
		for(int j = 1; j < path.size(); j++) {
			//Makes sure it doesn't check past the forward-moving-cell.
			if(path.size() - j <= i+1) {
				break;
			}
			//Checks whether the cells can see eachother.
			if(canSee(path[i], path[path.size() - j]) || path[i] == path[path.size() - j]) {
				//Erase the cells between 2 cells that see eachother
				path.erase(path.begin()+i+1, path.begin()+(path.size() - j));
				goto optimizePathRestart;
			}
		}
	}
}

The traversal of the initial optimized path with jumps in between nodes is shown below. The filled in version of the optimized path is also shown, using the same algorithm from 2.2.

3. The Disadvantages

3.1 Map Size / Terrain

As the map gets larger, the odds of any particular randomly selected cell having sightline to the last node at the end of the path become increasingly slim. This is also worsened depending on the layout of the walls. This is by and large the biggest downside of this pathfinder, and of all random pathfinders.

The visualizations shown thus far demonstrate Fast Random Pathfinder in a maze where there is only 1 path to the exit (recursive maze generation with a depth of 2). This, in some ways, is actually optimal in regard to ensuring that the path that is found is (almost) the perfect and shortest path. Whether or not this is actually the most effecient path is covered in 3.2.

3.2 Impossible Optimizations

On the left, you can see the optimizations that you'd expect labelled with blue arrows, but the path actually taken is shown with red arrows.

During optimization, Fast Random Pathfinder only cares whether an earlier node can see a later node, and trashes any nodes in between. However, there are circumstances where the nodes that are trashed actually held the key to what could've been a slightly faster route. This happens most frequently when optimizing around corners that split into 2 different paths. This causes Fast Random Pathfinder to overshoot occasionally.

Shown below is the previous example's true optimized path. Finding this path is impossible with the linear-approach that Fast Random Pathfinder uses, as it would require testing which optimizations are actually the most optimal.

3.3 Worst Case Runtime

The most glaring issue with Fast Random Pathfinder is the main reason no one would ever actually use a random pathfinder, fast or slow. The path to the goal is randomly generated, meaning that, worse-case, Fast Random Pathfinder is $ O(\infty) $. There is definitely some math that could be done to determine how probable it is that Fast Random Pathfinder finds a given path in a given environment after a certain number of iterations, but such efforts are not explored here.

4. Bonus: Maze Generation

Alongside developing Fast Random Pathfinder, I also implemented a maze generator to test it out. I have explored maze generation previously using recursive backtracking, but I encountered memory issues (it was also just a poor implementation) that resulted in imperfections.

This time, I implemented backtracking using stacks instead of recursion. This yielded much better results. Below is an example of backtracking maze generation with a depth of 2.

(back to top)